autovi: Automated Assessment of Residual Plots Using Computer Vision
useR! 2024
Weihao (Patrick) Li
Monash University
📝Overview
- Brief introduction to lineup
- Outline of the computer vision model
autoviPackage- Shiny app demo
🔍Regression Diagnostics
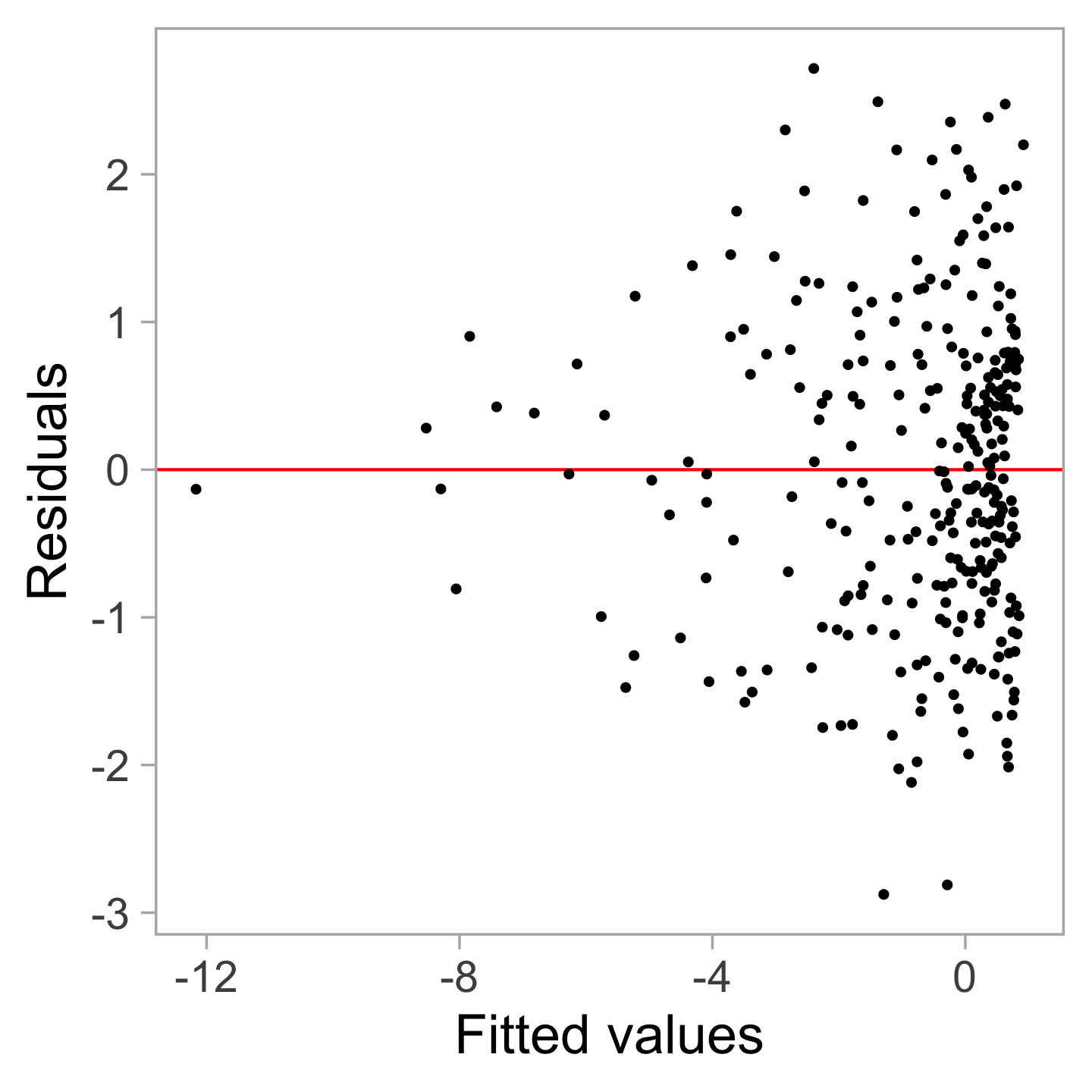
Diagnostics are the key to determining whether there is anything importantly wrong with a regression model.
e⏟Residuals=y⏟Observations−f(x)⏟Fitted values
Graphical approaches (plots) are the recommended methods for diagnosing residuals.
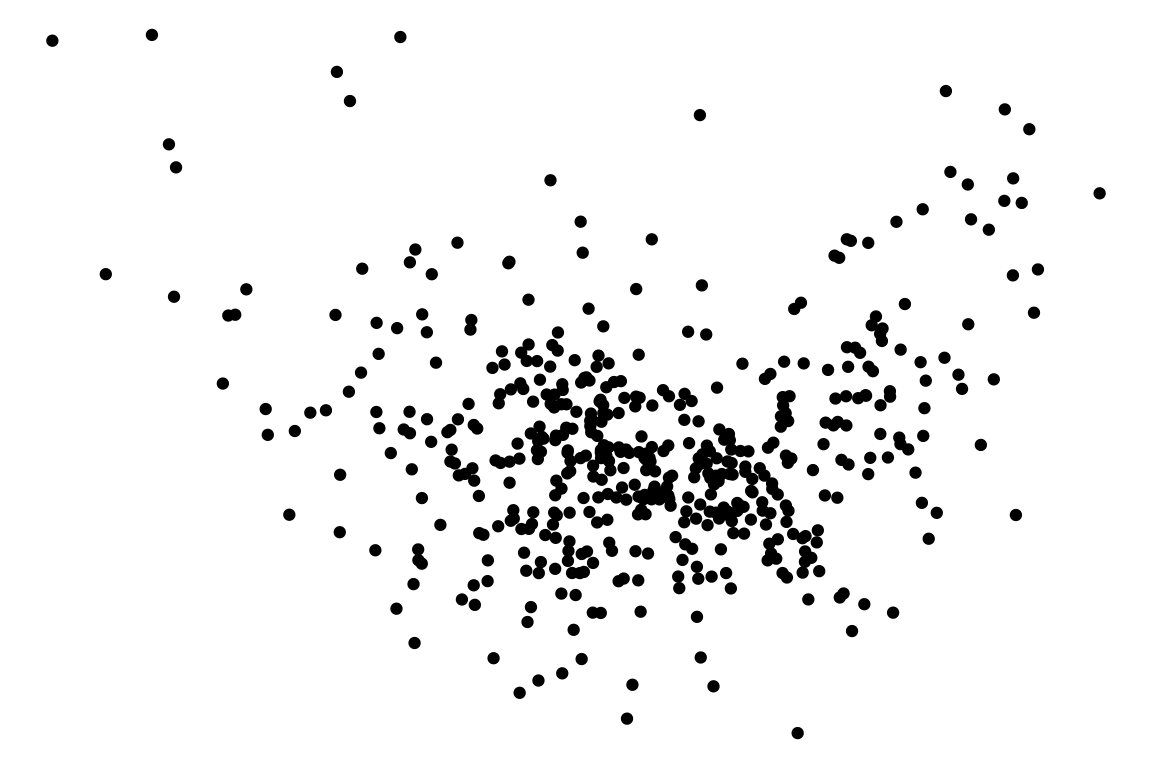
🤔Challenges
Vertical spread of the points varies with the fitted values indicates the existence of heteroskedasticity.
However, this is an over-interpretation.
The visual pattern is caused by a skewed distribution of the predictor.
🔬Visual Inference
The reading of residual plots can be calibrated by an inferential framework called visual inference (Buja, et al. 2009).
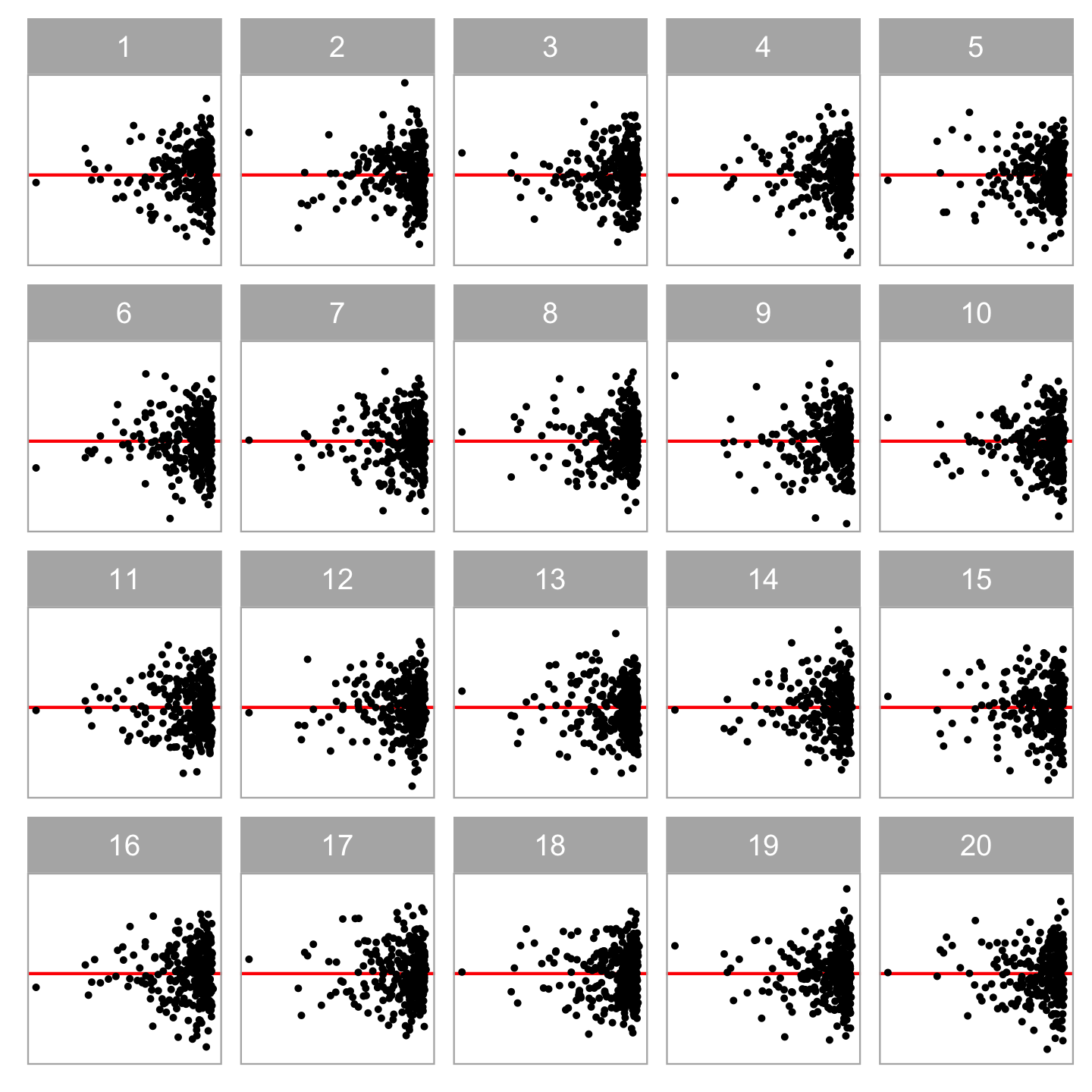
Typically, a lineup of residual plots consists of
- one actual residual plot
- 19 null plots containing residuals simulated from the fitted model.
To perform a visual test
- Observer(s) will be asked to select the most different plot(s).
- The p-value can be calculated using the beta-binomial model (VanderPlas et al., 2021).
🚫Limitations of Lineup Protocol
- Human can not
- evaluate lineup consisted of a large number of plots.
- evaluate a large number of lineups.
- Evaluation of lineup is high in labour cost and time consuming.
🤖Computer Vision Model
Modern computer vision models are well-suited for addressing this challenge.
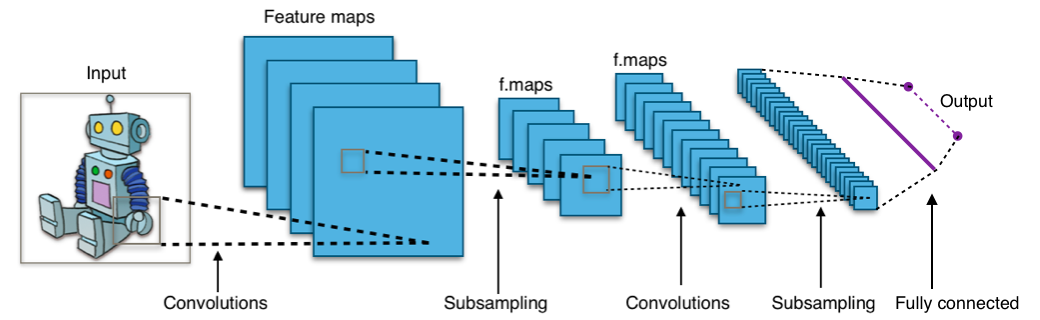
Source: https://en.wikipedia.org/wiki/Convolutional_neural_network
📏Measure the Difference
To develop computer vision models assessing lineups of residual plots, we need to define a numerical measure of “difference” or “distance” between plots.
- pixel-wise sum of square differences
- Structural Similarity Index Measure (SSIM)
- scagnostics
- …
📏KL Divergence of P from Q
We defined a distance measure based on Kullback-Leibler divergence to quantify the extent of model violations
D=log(1+∫Rnlogp(e)q(e)p(e)de),
P: reference residual distribution assumed under correct model specification.
Q: actual residual distribution.
D=0 if and only if P≡Q.
However, Q is typically unknown ⇒ D can not be computed.
🎯Estimation of the Distance
We can train a computer vision model to estimate D with a residual plot
ˆD=fCV(Vh×w(e,ˆy)),
where Vh×w(.) is a plotting function that saves a residual plot as an image with h×w pixels, and fCV(.) is a computer vision model which predicts distance in [0,+∞).
🔬Statistical Testing
The null distribution can be estimated by predicting ˆD for a large number of null plots.
The critical value can be estimated by the sample quantile (e.g. Qnull(0.95)) of the null distribution.
The p-value is the proportion of null plots having estimated distance greater than or equal to the observed one.
💡Training: Various Model Violations
Non-linearity + Heteroskedasticity
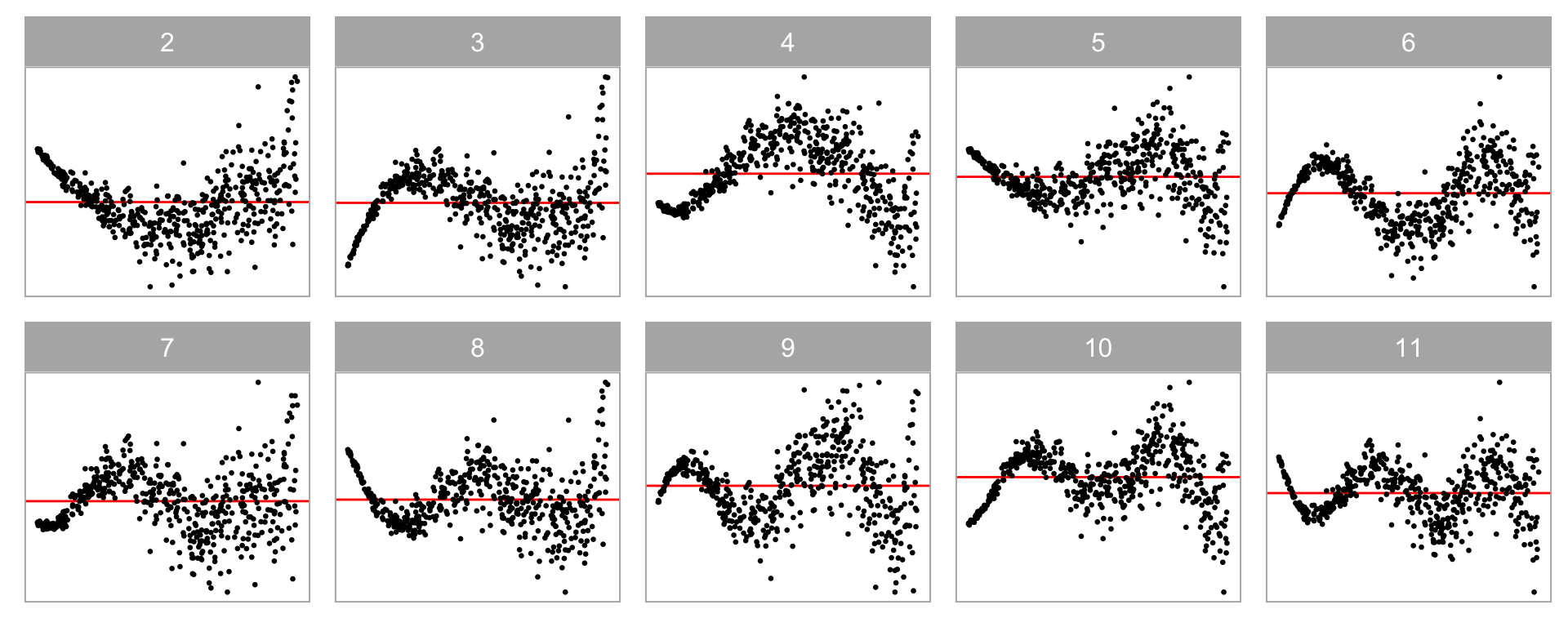
Non-normality + Heteroskedasticity
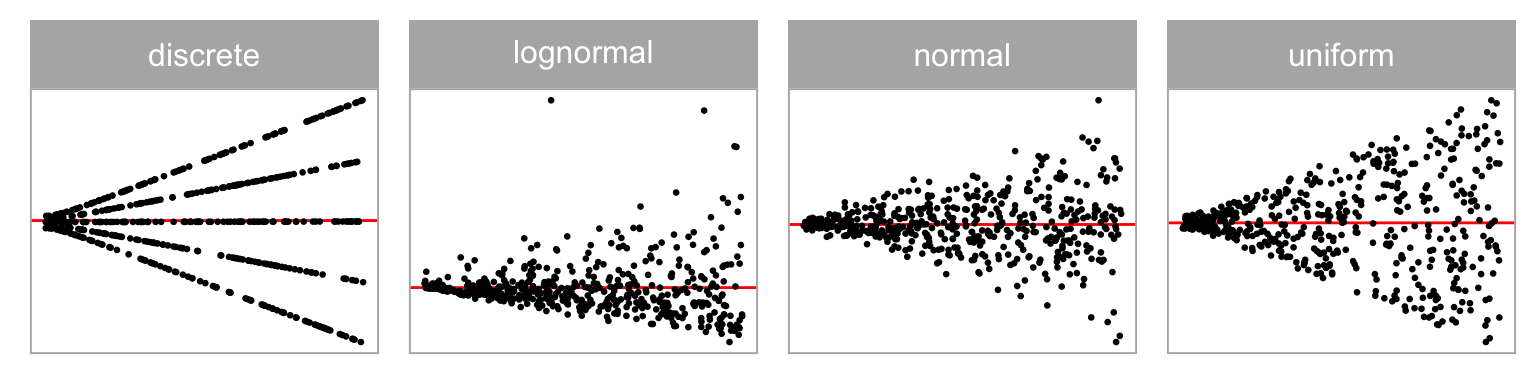
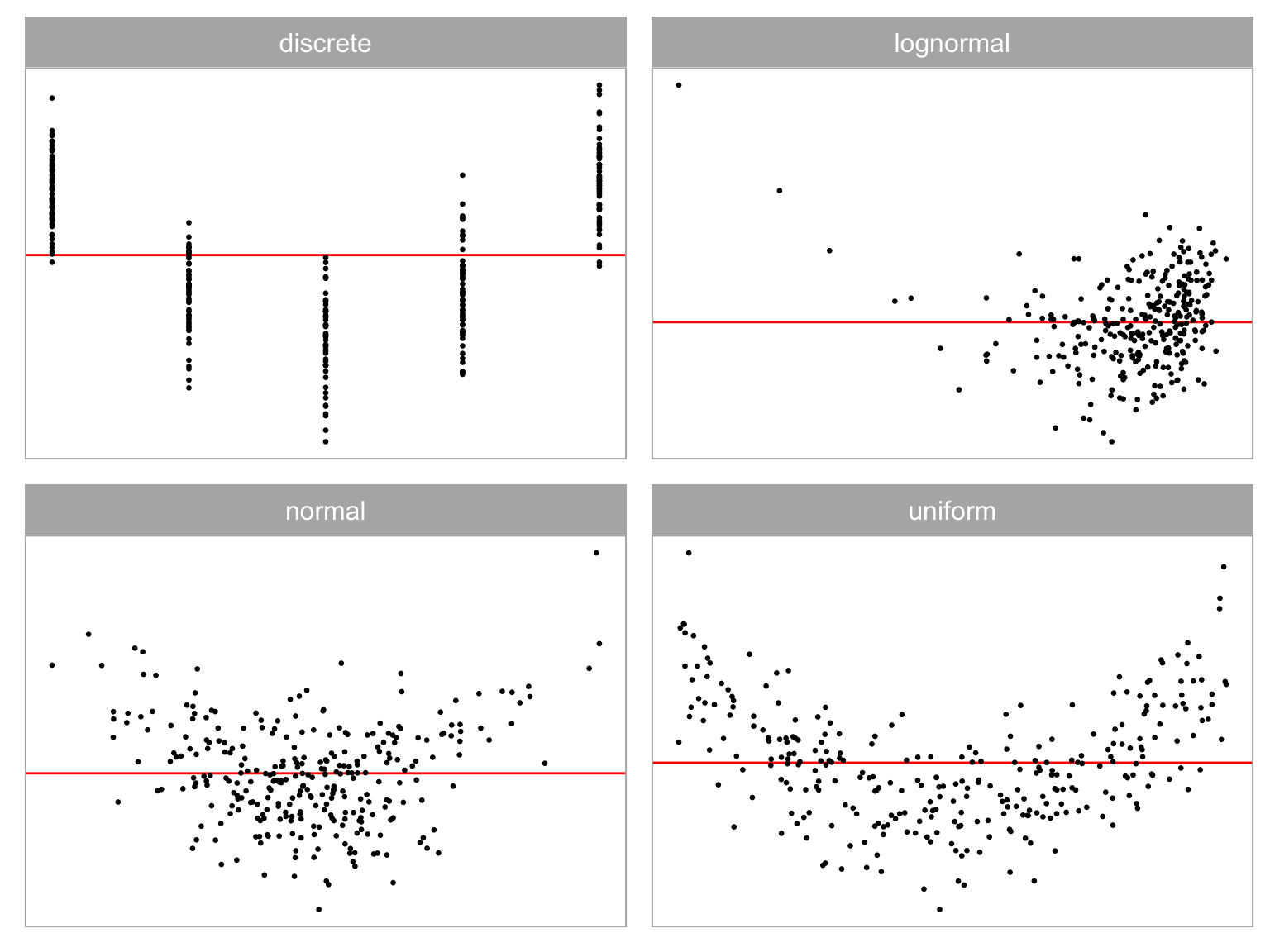
💡Training: Predictor Distribution
Distribution of predictor
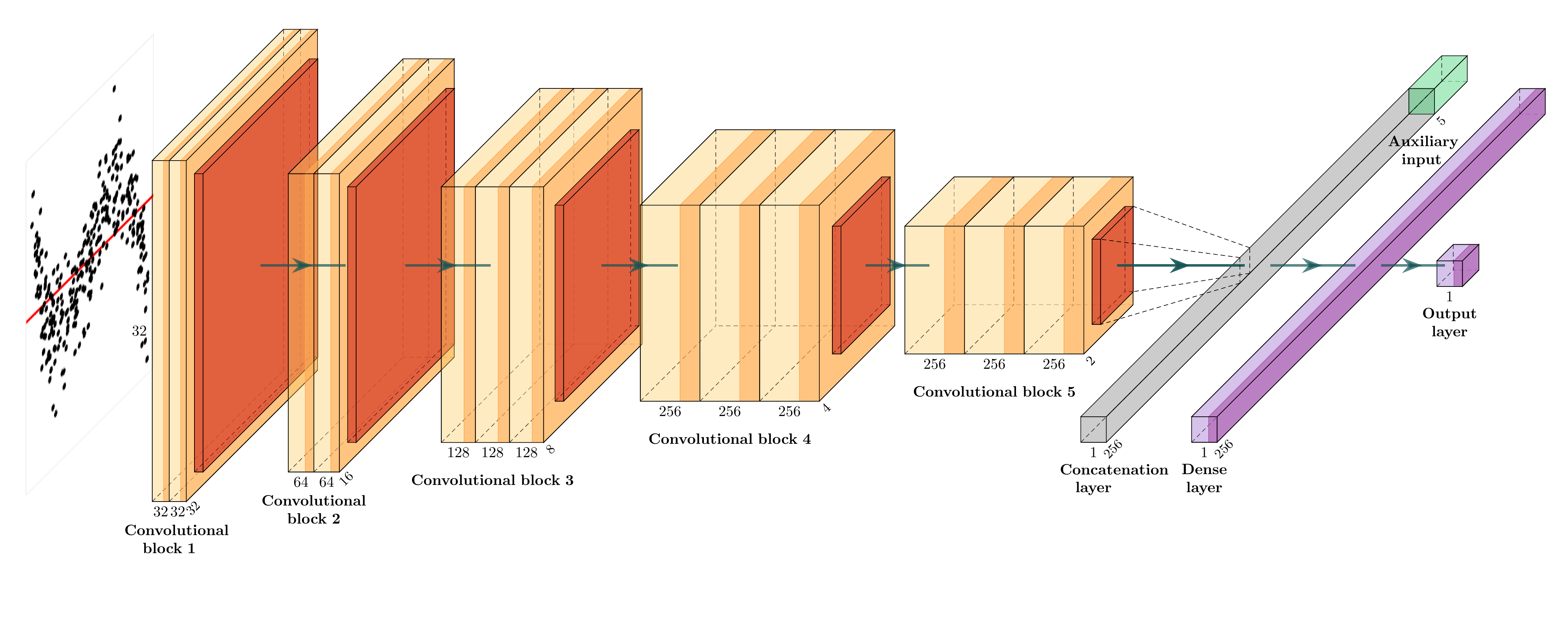
🏛️Model Architecture
The architecture of the computer vision model is adapted from VGG16 (Simonyan and Zisserman 2014).
autovi Package
The autovi package provides automated visual inference with computer vision models. It is available on CRAN and Github.
Core Methods
- Null residuals simulation:
rotate_resid() - Visual signal strength:
vss() - Comprehensive checks:
check()andsummary_plot()
💡Example: Boston Housing
rotate_resid()
Null residuals are simulated from the fitted model assuming it is correctly specified.
checker <- auto_vi(fitted_model = fitted_model,
keras_model = get_keras_model("vss_phn_32"))
checker$rotate_resid()# A tibble: 489 × 2
.fitted .resid
<dbl> <dbl>
1 632372. -33577.
2 525177. -82367.
3 646753. -118729.
4 624848. 109398.
5 611817. -12821.
6 551051. -1565.
7 504757. 54195.
8 445700. -70041.
9 281912. 13595.
10 453398. 64136.
# ℹ 479 more rows vss()
Visual signal strength of the actual residual plot
✔ Predict visual signal strength for 1 image.# A tibble: 1 × 1
vss
<dbl>
1 6.48 check()
── <AUTO_VI object>
Status:
- Fitted model: lm
- Keras model: (None, 32, 32, 3) + (None, 5) -> (None, 1)
- Output node index: 1
- Result:
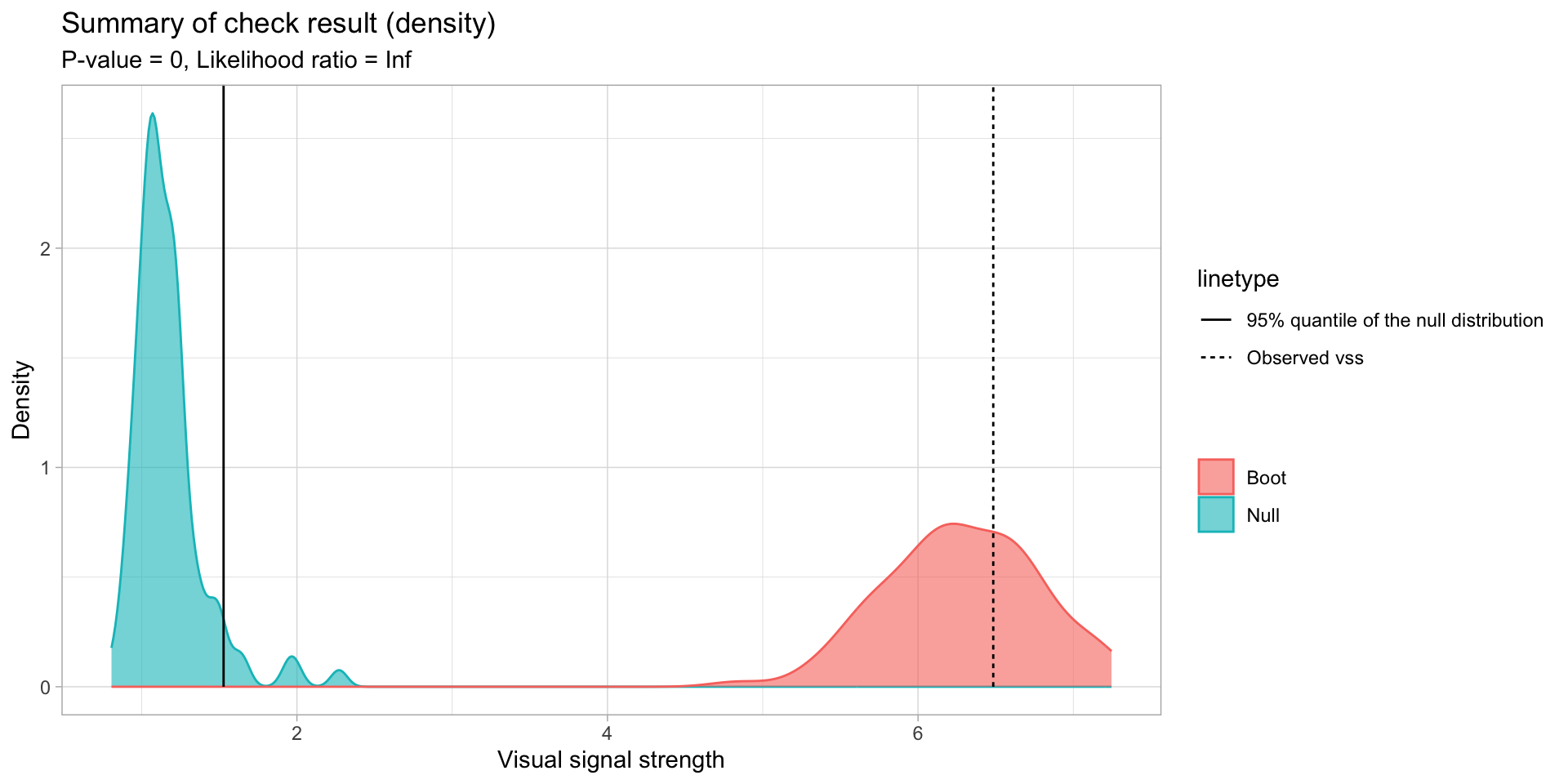
- Observed visual signal strength: 6.484 (p-value = 0)
- Null visual signal strength: [100 draws]
- Mean: 1.169
- Quantiles:
╔══════════════════════════════════════════╗
║ 25% 50% 75% 80% 90% 95% 99% ║
║1.037 1.120 1.231 1.247 1.421 1.528 1.993 ║
╚══════════════════════════════════════════╝
- Bootstrapped visual signal strength: [100 draws]
- Mean: 6.28 (p-value = 0)
- Quantiles:
╔══════════════════════════════════════════╗
║ 25% 50% 75% 80% 90% 95% 99% ║
║5.960 6.267 6.614 6.693 6.891 7.112 7.217 ║
╚══════════════════════════════════════════╝
- Likelihood ratio: 0.7064 (boot) / 0 (null) = Extremely large summary_plot()
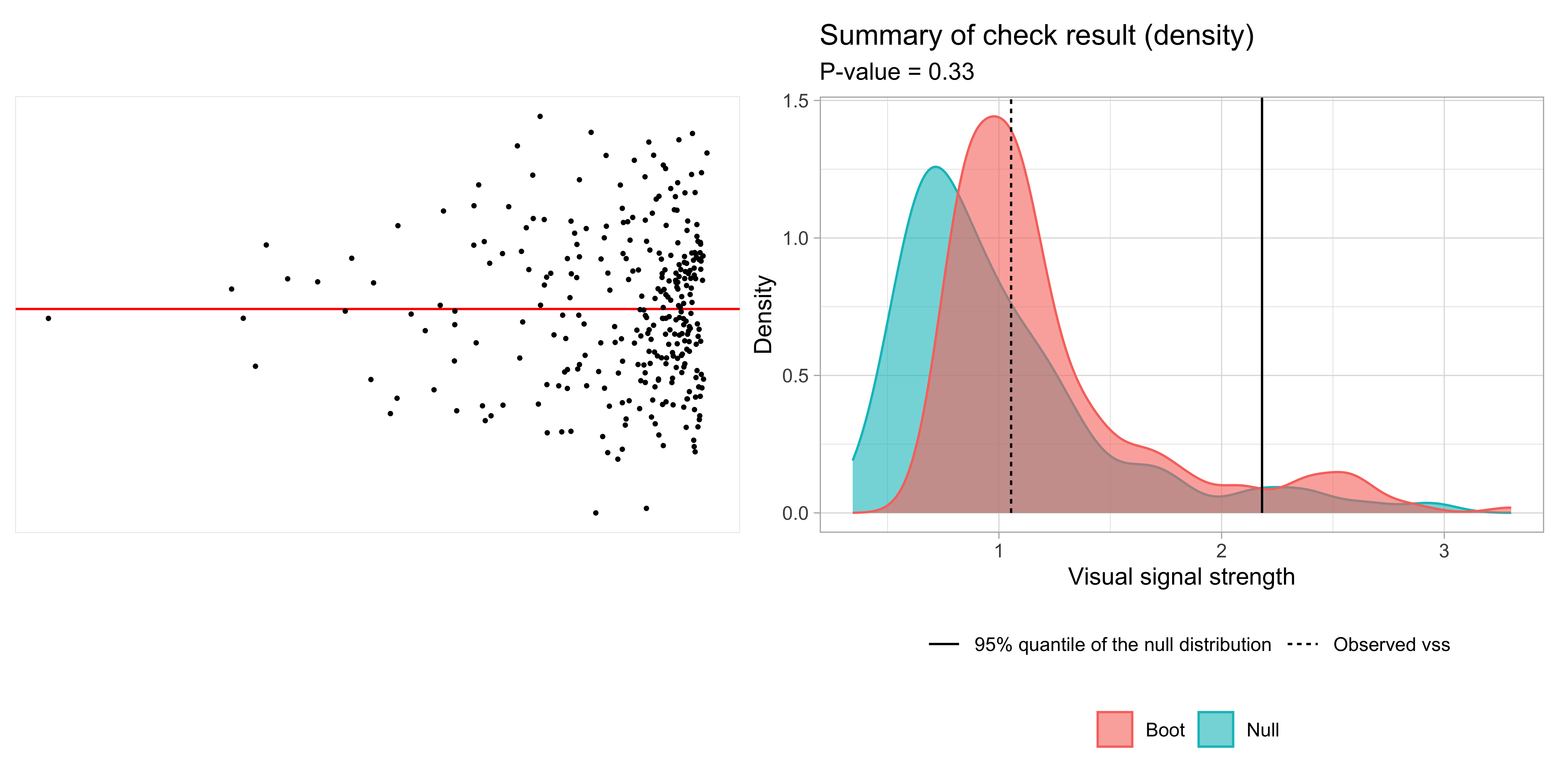
💡Example: Left-triangle
Breusch–Pagan test p-value = 0.0457
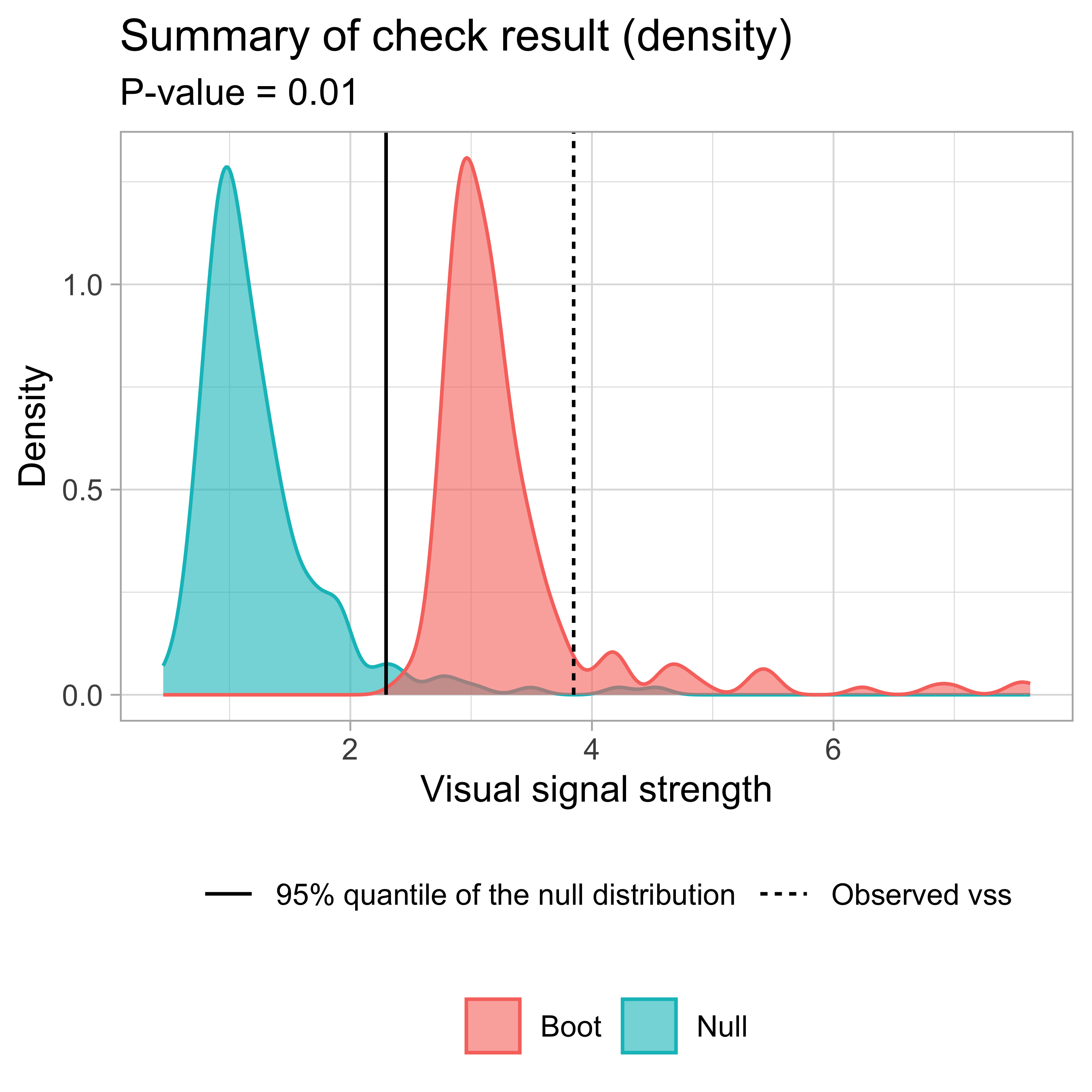
💡Example: Dinosaur
Ramsey Regression Equation Specification Error test p-value = 0.742
Breusch–Pagan test p-value = 0.36
Shapiro-Wilk test p-value = 9.21e-05
🌐Shiny Application
Don’t want to install TensorFlow?
Try our shiny web application: https://shorturl.at/DNWzt
🧩Extensions
To diagnose models other than the Classical Normal Linear Regression Model (CNLRM), one can:
- Use raw residuals, but be aware that violations may not be identifiable and the test could be two-sided.
- Use transformed residuals that are roughly normally distributed.
- Reuse the pre-trained convolutional blocks and train a new computer vision model with an appropriate distance measure.
🎬Takeaway
You can use autovi to
Evaluate lineups of residual plots of linear regression models
Captures the magnitude of model violations through visual signal strength
Automatically detect model misspecification using a visual test
Thanks! Any questions?
🔗Relevant links

Slides URL: https://autovi.netlify.app